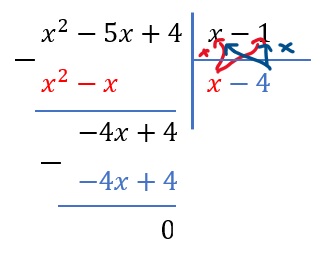1 Quy tắc
- Ví dụ : Nhân đa thức x-2 với đa thức 6x2-5x+1
- Gợi ý + Hãy nhân mỗi hạng tử của đa thức x-2 với đa thức 6x2-5x+1
+ Hãy cộng các kết quả vừa tìm được ( chú ý dấu của các hạng tử )
- Hướng dẫn
(x-2)(6x2-5x+1)=x(6x2-5x+1)-2(6x2-5x+1)
=x6x2+x(-5x)+x1+(-2)6x2+(-2)(-5x)+(-2)1
=6x3-5x2+x-12x2+10x-2
=6x3-17x2+11x-2
- Ta nói đa thức 6x3-17x2+11x-2 là tích của đa thức x-2 và đa thức 6x2-5x+1
- Tổng quát , ta có quy tắc nhân đa thức với đa thức như sau : Muốn nhân một đa thức với một đa thức , ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau
==) Nhận xét : Tích của hai đa thức là một đa thức
(?) Nhân đa thức xy-1 với đa thức x3-2x-6
- Hướng dẫn :
Ta có: (xy-1)(x3-2x-6)
=xy(x3-2x-6)-1.(x3-2x-6)
=xy.x3-xy.2x-xy.6-(x3-2x-6)
=xy.x3-xy.2x-xy.6-x3+2x+6
=x4y-x2y-3xy-x3+2x+6
=x4y-x3-x2y-3xy+2x+6
- Chú ý : Khi nhân đa thức của một biến ở ví dụ trên , ta còn có thể trình bày như sau :
| 6x2-5x+1 | |
| x-2 | |
| -12x2+10x-2 | |
| 6x3-5x2+x | |
| 6x3-17x2+11x-2 |
- Ở cách này , trước kết quả ta phải sắp xếp các đa thức theo lũy thừa giảm dần hoặc tăng dần của biến, sau đó trình bày như sau :
- Đa thức này viết dưới đa thức kia
- Kết quả của phép nhân mỗi hạng tử của đa thức thứ hai với đa thức thức nhất được viết riêng trong 1 dòng
- Các đơn thức đồng dạng được xếp vào cùng một cột
- Cộng theo từng cột
2 Áp dụng
(?) làm tính nhân
a) (x+3)(x2+3x-5)
b) (xy-a)(xy+5)
- Hướng dẫn :
a) (x + 3)(x2 + 3x – 5)
= x.(x2 + 3x – 5) + 3.(x2 + 3x – 5)
= x.x2 + x.3x + x.(–5) + 3.x2 + 3.3x + 3.(–5)
= x3 + 3x2 – 5x + 3x2 + 9x – 15
= x3 + (3x2 + 3x2) + (9x – 5x) – 15
= x3 + 6x2 + 4x – 15.
b) (xy – 1)(xy + 5)
= xy.(xy + 5) + (–1).(xy + 5)
= xy.xy + xy.5 + (–1).xy + (–1).5
= x2y2 + 5xy – xy – 5
= x2y2+ 4xy – 5.
(?) Viết biểu thức tính diện tích của 1 hình chữ nhật theo x và y , biết 2 kích thước của hình chữ nhật đó là (2x+y) và (2x-y)
- Áp dụng : Tính diện tích của hình chữ nhật khi x=2,5 mét và y=1 mét
- Hướng dẫn :
Biểu thức tính diện tích hình chữ nhật là:
S = (2x + y).(2x – y)
= 2x.(2x – y) + y.(2x – y)
= 2x.2x + 2x.(–y) + y.2x + y.(–y)
= 4x2 – 2xy + 2xy – y2
= 4x2 – y2
Áp dụng : khi x = 2,5 mét và y = 1 mét
⇒ S = 4.2,52 – 12 = 4.6,25 – 1 = 25 – 1 = 24
Vậy diện tích của hình chữ nhật là: 24 mét vuông
Bài tập
7. làm tính nhân
a) (x2-2x+1)(x-1)
b) (x3-2x2+x-1)(5-x)
- Hướng dẫn :
a) (x2 – 2x + 1)( x – 1)
= x2.(x – 1) + (–2x).(x – 1) + 1.(x – 1)
= x2.x + x2.(– 1) + (– 2x).x + (–2x).(–1) + 1.x + 1.(–1)
= x3 – x2 – 2x2 + 2x + x – 1
= x3 – (x2 + 2x2) + (2x + x) – 1
= x3 – 3x2 + 3x – 1
b) (x3 – 2x2 + x – 1)(5 – x)
= (x3 – 2x2 + x – 1).5 + (x3 – 2x2 + x – 1).(–x)
= x3.5 + (–2x2).5 + x.5 + (–1).5 + x3.(–x) + (–2x2).(–x) + x.(–x) + (–1).(–x)
= 5x3 – 10x2 + 5x – 5 – x4 + 2x3 – x2 + x
= –x4 + (5x3 + 2x3) – (10x2 + x2) + (5x + x) – 5
= –x4 + 7x3 – 11x2 + 6x – 5
Ta có:
(x3 – 2x2 + x – 1).(x – 5)
= (x3 – 2x2 + x – 1).[–(5 – x)]
= – (x3 – 2x2 + x – 1).(5 – x)
= – (–x4 + 7x3 – 11x2 + 6x – 5)
= x4 – 7x3 + 11x2 – 6x + 5.
8. Làm tính nhân :
a) (x2y2-xy+2y)(x-2y)
b) (x2-xy+y2)(x+y)
- Hướng dẫn :
a) = (x2y2 - xy + 2y)(x – 2y)
= x3y2-2x2y3-().x2y + xy2 + 2xy - 4y2
b) = (x2 – xy + y2)(x + y)
= x3 + x2y – x2y – xy2 + xy2 + y3
= x3 + y3
9. Điền kết quả tính được vào bảng :
| Giá trị của x và y |
Giá trị của biểu thức (x-y)(x2+xy+y2) |
| x=-10; y=2 | |
| x=-1; y=0 | |
| x=2; y=-1 | |
| x=-0,5; y=1,25 | |
| Trường hợp cuối có thể dùng máy tính bỏ túi để tính. | |
- Hướng dẫn :
A = (x – y).(x2 + xy + y2)
= x.(x2 + xy + y2) + (–y).(x2 + xy + y2)
= x.x2 + x.xy + x.y2 + (–y).x2 + (–y).xy + (–y).y2
= x3 + x2y + xy2 – x2y – xy2 – y3
= x3 – y3 + (x2y – x2y) + (xy2 – xy2)
= x3 – y3.
Tại x = –10, y = 2 thì A = (–10)3 – 23 = –1000 – 8 = –1008
Tại x = –1 ; y = 0 thì A = (–1)3 – 03 = –1 – 0 = –1
Tại x = 2 ; y = –1 thì A = 23 – (–1)3 = 8 – (–1) = 9
Tại x = –0,5 ; y = 1,25 thì A = (–0,5)3 – 1,253 = –0,125 – 1,953125 = –2,078125
Vậy ta có bảng sau :
| Giá trị của x và y |
Giá trị của biểu thức (x-y)(x2+xy+y2) |
| x=-10; y=2 | -1008 |
| x=-1; y=0 | -1 |
| x=2; y=-1 | 9 |
| x=-0,5; y=1,25 | –2,078125 |
Luyện tập
10. Thực hiện phép tính :
a) (x2-2x+3)(x-5)
b) (x2-2xy+y2)(x-y)
- Hướng dẫn :
a) (x2-2x+3)(x-5)
= (x2-2x+3).x+(x2-2x+3)..(-5)
= x2.x+(-2x).x+3.x+x2.(-5)+(-2x).(-5)+3.(-5)
=x3-x2+x-5x2+10x-15
=x3-(x2+5x2)+(x+10x)-15
=x3-6x2+x-15
b) (x2-2xy+y2)(x-y)
= (x2 – 2xy + y2).x + (x2 – 2xy + y2).(–y)
= x2.x + (–2xy).x + y2.x + x2.(–y) + (–2xy).(–y) + y2.(–y)
= x3 – 2x2y + xy2 – x2y + 2xy2 – y3
= x3 – (2x2y + x2y) + (xy2 + 2xy2) – y3
= x3 – 3x2y + 3xy2 – y3.
11. Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:
(x-5)(2x+3)-2x(x-3)+x+7
- Hướng dẫn :
Có: (x - 5)(2x + 3) - 2x(x - 3) + x +7
= 2x2 - 10x + 3x - 15 - 2x2 + 6x + x + 7
= (2x2 - 2x2) - (10x - 3x - 7x - x) - (15 - 7)
= 0 - 0 - 8
= -8
Vậy giá trị của biểu thức trên không phụ thuốc vào biến x
- Hướng dẫn :
Rút gọn biểu thức:
A = (x2 – 5)(x + 3) + (x + 4)(x – x2)
= x2.(x + 3) + (–5).(x + 3) + x.(x – x2) + 4.(x – x2)
= x2.x + x2.3 + (–5).x + (–5).3 + x.x + x.(–x2) + 4.x + 4.(–x2)
= x3 + 3x2 – 5x – 15 + x2 – x3 + 4x – 4x2
= (x3 – x3) + (3x2 + x2 – 4x2) + (4x – 5x) – 15
= –x – 15.
a) Nếu x = 0 thì A = –0 – 15 = –15
b) Nếu x = 15 thì A = –15 – 15 = –30
c) Nếu x = –15 thì A = –(–15) – 15 = 15 – 15 = 0
d) Nếu x = 0,15 thì A = –0,15 – 15 = –15,15
13. Tìm x , biết :
(12x-5)(4x-1)+(3x-7)(1-16x)=81
- Hướng dẫn :
VT = (12x – 5)(4x – 1) + (3x – 7)(1 – 16x)
= 12x.(4x – 1) + (–5).(4x – 1) + 3x.(1 – 16x) + (–7).(1 – 16x)
= 12x.4x+ 12x.(–1) + (–5).4x + (–5).(–1) + 3x.1 + 3x.(–16x) + (–7).1 + (–7).(–16x)
= 48x2 – 12x – 20x + 5 + 3x – 48x2 – 7 + 112x
= (48x2 – 48x2) + (– 12x – 20x + 3x + 112x) + (5 – 7)
= 83x – 2
Vậy ta có:
83x – 2 = 81
83x = 81 + 2
83x = 83
x = 83 : 83
x = 1.
14. Tìm ba số tự nhiên chẵn liên tiếp , biết tích của hai số sau lớn hơn tích của hai số đầu là 192
- Hướng dẫn :
gọi ba số tự nhiên chẵn liên tiếp đó là a,a+2,a+4 (a∈∈N)
Có: tích của hai số sau lớn hơn tích của 2 số đầu là 192
=> (a+2)(a+4)-(a+2)a=192
a2+4a+2a+8-a2-2a=192
(a2-a2)+(4a+2a-2a)+8=192
4a=192-8
4a=184
a=46
=> {a+2=46+2=48,a+4=46+4=50}
vậy ba số tự nhiên chẵn liên tiếp cần tìm lần lượt là: 46,48,50
15. Làm tính nhân
a) (x+y)(x+y)
b) (x-y)(x-y)
- Hướng dẫn
a) (x+y)(x+y)
=x(x+y)+y.(x+y)
=x.x+x.y=y.x+y.y
=x2+xy+xy+y2
=x2+xy+y2
b) (x-y)(x-y)
=x(x-y)+(-y)(x-y)
=x.x+x.(-y)+(-y).x+(-y).(-y)
=x2-xy-xy+y2
=x2-xy+y2
Bài học/ Tin tức liên quan của bài học/tin tức trong bộ sách Chương trình hiện hành
Chứng minh giá trị biểu thức không phụ thuộc vào X
Bài toán chứng minh giá trị biểu thức không phụ thuộc vào x thuộc chương trình Đại số 8
Chuyên đề 1 – Hằng đẳng thức đáng nhớ
Chuyên đề 1 – Hằng đẳng thức đáng nhớ
Chuyên đề 3 – Phân tích đa thức thành nhân tử
Bản chất : Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

Chuyên đề 7 – Giải bài toán bằng cách lập phương trình
Các bài tập, bài toán tự giải bằng cách lập phương trình dành cho học sinh lớp 8.
Bài 5. Phương trình chứa ẩn ở mẫu
Giá trị tìm được của ẩn có là nghiệm của phương trình đã cho hay không?