1. Định lý đảo
?.1 Tam giác ABC có AB = 6cm; AC = 9cm
Lấy trên canh AB điền B, trên cạnh AC điểm C' sao cho AB'= 2cm; AC'= 3cm (h.8).
1.) So sánh cảc tỉ sổ và .
2.) Vẽ đường thẳng a di qua B' và song song với BC, đường thẳng a cắt AC tại điểm C".
a)Tinh dộ dài đoạn thẳng AC".
b) Có nhận xét gì về C' và C" và về hai đường thắng BC và BC'?
Ta thừa nhận không chứng minh định lí đảo sau đây:
Định lí Ta-lét đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thắng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam
| GT |
ABC, B' AC |
| KL |
a) Trong hình đã cho có bao nhiêu cặp đường thẳng song song với nhau?
b) Tứ giác BDEF là hinh gì ?
c) So sánh các tỉ số AD/AB; AE/AC; DE/BC và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác ADE và ABC.
2. Hệ quả của định lí Ta-lét
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó sẽ tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
| GT |
ABC B'C' // BC (B' AB, C' AC) |
| KL |
Chứng minh
- Vì B'C'/BC (h.10) nên theo định lí Ta-lét ta có:
- Từ C' kẻ C'D//AB (DBC) nên theo định lí Ta-lét ta có:
- Tứ giác B’C’DB là hình bình hành (vì có các cặp cạnh đối song song) nên ta có:
B'C'DB
- Từ (1) và (2) thay BD bằng B’C’ ta có:
Chú ý
Hệ quả trên vấn đúng cho trường hợp đường thẳng a song song với một cạnh của tam giác và cắt phần kéo dài của hai canh còn lại (h.lI):
? 3 Tính độ dài x của các đoan thẳng trong hình 12.
Hình 12
BÀI TẬP
6. Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song.
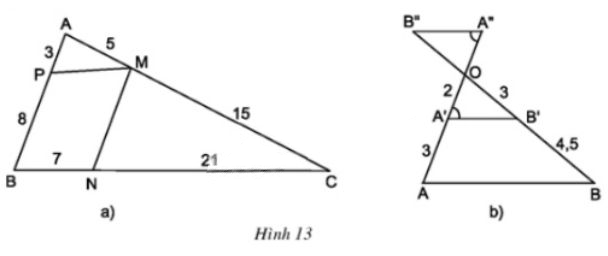
Hướng dẫn giải:
Trong hình 13a:
; vì nên
⇒ PM và BC không song song. (Theo định lí Talet đảo)
Ta có
=>
=> MN // AB (Theo định lí Talet đảo)
Trong hình 13b:
Ta có: ;
=>
=> A'B' // AB (Theo định lí Talet đảo) (1)
Có
Mà hai góc và ở vị trí so le trong
Suy ra A"B" // A'B' (2)
Từ (1) và (2) suy ra AB // A'B'//A''B''??A''B//A''B''
7. Tính các độ dài x, y trong
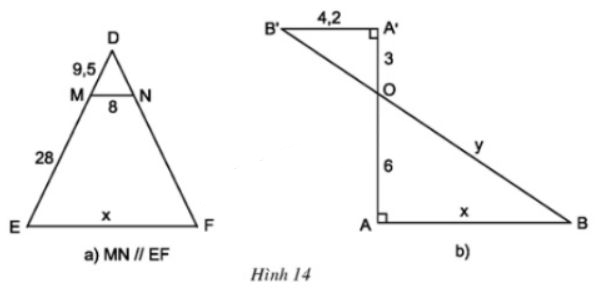
Hướng dẫn giải: Trong hình 14a
MN//EF, theo hệ quả định lí Ta-lét ta có:
MNEF=MDDE
Mà DE=MD+ME=9,5+28=37,5
⇒8x=9,537,5
⇒x=8.37,59,5=60019≈31,6
* Trong hình 14b
Ta có A′B′⊥ AA′ (giả thiết) và AB⊥AA′
⇒A′B′//AB (từ vuông góc đến song song)
⇒A′OOA=A′B′AB (Theo hệ quả định lí Ta-let)
hay 36=4,2x
x=6.4,23=8,4
ΔABO ∆ vuông tại A nên áp dụng định lý Pitago ta có:
y2=OB2=OA2+AB2⇒y2=62+8,42=106,56⇒y= 10,3
8. a) Để chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau, người ta đã làm như hình 15.
Hãy mô tả cách làm trên và giải thích vì sao các đoạn thằng AC, CD, DB bàng nhau.
b) Bằng cách làm tương tự, hãy chia đoan thẳng AB cho trước thành 5 đoạn bằng nhau. Hỏi có cách nào khác Với cách làm như trên mà vẫn có thế chia đoạn thẳng AB cho trước thành 5 đoạn thẳng bằng nhau?
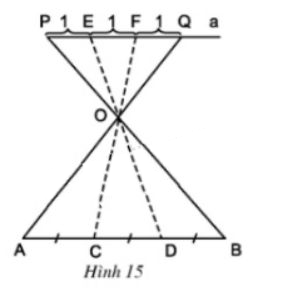
Hướng dẫn giải: Mô tả cách làm:
Vẽ đoạn PQ song song với AB, có độ dài bằng 33 đơn vị
- Trên PQ lấy lần lượt các điểm E, F sao cho PE=EF=FQ=1 đơn vị
- Xác định giao điểm O của hai đoạn thẳng PB và QA.
- Vẽ các đường thẳng EO,FO cắt AB tại C và D.
Chứng minh AC=CD=DB
ΔOPE và ΔOBD có PE//DB (theo cách vẽ) nên DBPE=ODOE (1) (hệ quả định lý TaLet)
ΔOEF và ΔODC có EF//CD (theo cách vẽ) nên CDEF=ODOE=OCOF (2) (hệ quả định lý TaLet)
ΔOFQ và ΔOCA có FQ//AC (theo cách vẽ) nên ACFQ=OCOF (3) (hệ quả định lý TaLet)
Từ (1), (2) và (3) suy ra:
DBPE=CDEF=ACFQ mà PE=EF=FQ (gt) nên DB=CD=AC.
Vây: DB=CD=AC.
9. Cho tam giác ABC và điếm D trên canh AB sao cho AD = 13.5cm, DB = 4,5cm. Tính tỉ số các khoảng cách từ các điểm D và B đến canh AC.
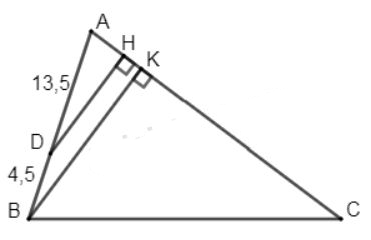
Hướng dẫn giải: Gọi DH và BK lần lượt là khoảng cách từ B và D đến cạnh AC.
Ta có DH//BK (vì cùng vuông góc với AC)
⇒DHBK=ADAB⇒ (theo hệ quả định lý Ta Let)
Mà AB=AD+DB (giả thiết)
⇒AB=13,5+4,5=18⇒=13,5+4,5=18 (cm)
Vậy DHBK=13,518=34=13,518=34
Vậy tỉ số khoảng cách từ điểm D và B đến AC bằng 3434
LUYỆN TẬP
10. Tam giác ABC có đườmg cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B, C’ và H’ (h.16).
a) Chứng minh rằng:
b) Áp dụng : Cho biết AH' = 1/3AH và diện tích tam giác ABC là 67,5cm2. Tính diện tích tam giác ΔAB′C′.
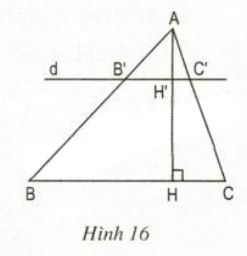
Hướng dẫn giải:
a, Vì B′C′//BC ⇒ (1) (theo hệ quả định lý TaLet)
Trong ΔABH∆ có B′H′//BH ⇒ (2) (theo hệ quả định lý TaLet)
Từ (1) và (2) ⇒
b, B′C′//BC mà AH⊥BC nên AH′⊥B′C′hay AH′ là đường cao của ΔAB′C.
Giả thiết: AH′=13AH.
Áp dụng kết quả câu a) ta có:
B′C′BC=AH′AH=13
⇒B′C′=13BC
SAB′C′ = AH′.B′C′
= .AH.BC
= ( AH.BC )
11. Tam giác ABC có BC = 15cm. Trên đường cao AH áy các diểm I, K sao cho AK= KI = IH. Qua I và K vẽ các đường EF//BC, MN//BC (h.17).
a) Tính đo dài các đoan thẳng MN và EF.
b) Tính diên tích tứ giác MNFE, biết rằng diện tích của tam giác ABC là 270cm2.
12. Có thể đo được chiều rộng của một khúc sông mà không cán phải sang bờ bên kia hay không ?
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cân phải sang bờ bên kia (h.18). Nhìn hình vẽ đã cho, hãy mộ tả những công việc cân làm và tính khoảng cách AB= x theo BC = a, B'C'= a', BB' =h
13. Cho ba đoạn thẳng có độ dài là m,n,p(cùng đơn vị đo).
Dựng đoạn thẳng có độ dài x sao cho:
a) x/m=2;
b) x/n=2/3;
c) m/x=n/p.
Vẽ hai tia Ox,
Trên tia Ox đặt đoạn thẳng OA=2 đon vi, OB= 3 đơn vị
Trên tia Oy đặt đoạn thảng 0B’ =n và xác đinh điểm A' sao cho
OA/ OB = OA’/OB’
- Từ đó ta có: OA’= x
Bài học/ Tin tức liên quan của bài học/tin tức trong bộ sách Chương trình hiện hành
Bài 3: Tính chất đường phân giác của tam giác
Đường phân giác của một góc trong tam giác cgia cạnh đối diện với gọc đó thành hai đoạn thẳng theo tỉ số nào?