A. LÝ THUYẾT
1. Đường trung bình của tam giác
Định nghĩa : Đường trung bình của tam giác là đoạn thẳng nối trung điểm của hai cạnh của tam giác.

Định lý 1.
| Đường thẳng đi qua trung điểm của một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba. |
Định lý 2.
| Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. |
2. Cách chứng minh đoạn thẳng là đường trung bình của tam giác
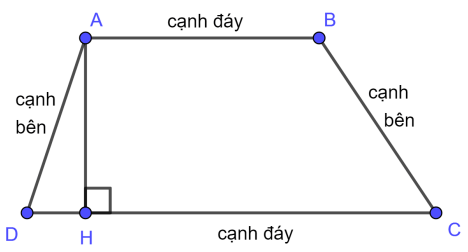
Có 2 cách : (hình minh họa ở trên)
Cách 1 : Chứng minh D là trung điểm của AB và E là trung điểm của AC à DE là đường trung bình của tam giác ABC.
Cách 2 : Chứng minh D là trung điểm của AB và DE song song với BC à DE là đường trung bình của tam giác ABC.
3. Đường trung bình của hình thang
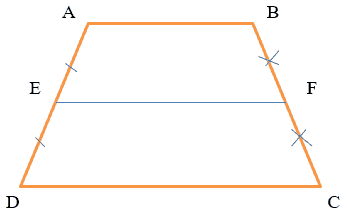
Định nghĩa : Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên của hình thang.
Định lý 3.
| Đường thẳng đi trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai. |
Định lý 4.
| Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy. |
4. Cách chứng minh đoạn thẳng là đường trung bình của hình thang
Có 2 cách chứng minh.
Cách 1 : Chứng minh E là trung điểm của AD và F là trung điểm của BC à EF là đường trung bình của hình thang ABCD.
Cách 2 : Chứng minh E là trung điểm của AD và EF // DC à EF là đường trung bình của hình thang ABCD.
B. BÀI TẬP
Bài toán 1 : Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh độ dài EK và CD, KF và AB.
b) Chứng minh rằng
Gợi ý :
– Học sinh tự vẽ hình.
– a) dựa vào tính chất đường trung bình trong tam giác.
– b) dựa vào ý a) đã chứng minh + bất đẳng thức trong tam giác.
Bài toán 2 : Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng :
a) EI // CD, IF // AB.
b)
Gợi ý : tương tự bài toán 1.
Bài toán 3 : Cho hình thang ABCD có đáy AB, CD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng ba điểm E, I, F thẳng hàng.
Gợi ý :
– Học sinh tự vẽ hình.
– chứng minh EI // DC và FI // DC suy ra EI trùng FI suy ra ba điểm thẳng hàng.
Bài toán 4 : Cho tam giác ABC, các trung tuyến BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE song song và bằng IK.
Gợi ý :
– Học sinh tự vẽ hình.
– Dựa vào dữ kiện đề bài cho + đường trung bình trong tam giác.
Bài toán 5 : Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD = DC. Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh rằng AI = IM.
Gợi ý :
– Học sinh tự vẽ hình.
– Gọi O là trung điểm của DC. Đi chứng minh MO // DI. Chứng minh tiếp DI là đường trung bình của tam giác AMO.
Bài học/ Tin tức liên quan của bài học/tin tức trong bộ sách Chương trình hiện hành
Định lí đảo và hệ quả của định Ií Ta-lét
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thắng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh...
Bài 3: Tính chất đường phân giác của tam giác
Đường phân giác của một góc trong tam giác cgia cạnh đối diện với gọc đó thành hai đoạn thẳng theo tỉ số nào?