I. Tóm tắt lý thuyết về Tập hợp
1. Cách viết tập hợp
• Tên tập hợp được viết bằng các chữ cái in hoa : A ; B ; C ;…
• Để viết tập hợp thường có hai cách :
– Liệt kê các phần tử của tập hợp
* Ví dụ : A = { 0 , 1 , 2 , 3}
– Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó
* Ví dụ : A = { x ∈ N | x < 4}
* Chú ý :
– Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ” (nếu có phần tử số “ ,” )
– Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý
2. Tập hợp các số tự nhiên
N = { 0; 1; 2 ; 3 ; 4 ;……}; N* = {1 ; 2 ; 3 ; 4; ……}
– Số 0 là số tự nhiên bé nhất
3. Số phần tử của một tập hợp
Một tập hợp có thể có một phần tử , có nhiều phần tử, có vô sô phần tử cũng có thể không có phần tử nào ( gọi là tập rỗng : )
VD : A = { x , y}; B = { bút , thước }; C = { 1; 2 ; 3; 4; …..; 100 }; D = {Ø}
4. Tập hợp con
– Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập hợp con của tập hợp B
– Kí hiệu : ⊂
5. Các dạng toán áp dụng
II. Các dạng toán về tập hợp
° Dạng 1 : Viết tập hợp
* Phương pháp:
– Liệt kê các phần tử của nó.
– Chỉ ra tính chất đặc trưng cho các phần tử của nó
* Bài tập vận dụng
♦ Bài toán 1 : A là tập hợp các số tự nhiên không quá 4
Viết tập hợp A bằng hai cách : liệt kê và chỉ ra tính chất đặc trưng của các phần tử
♦ Bài toán 2 : A là tập hợp các sô tự nhiên lớn hơn 5 và nhỏ hơn 9
Viết tập hợp A bằng hai cách : liệt kê và chỉ ra tính chất đặc trưng của các phần tử
♦ Bài toán 3: Cho các tập hợp.
A = { x ∈ N / x ≤ 7 }; B = { x ∈ N / x < 7 }; C = { x ∈ N / 6 < x < 7 }
Viết các tập hợp A , B ,C bằng cách liệt kê các phần tử và cho biết số phần tử của tập hợp
° Dạng 2: Tìm số phần tử của 1 tập hợp
* Phương pháp:
– Để đếm các số tự nhiên từ a đến b (2 số liên tiếp cách nhau d đơn vị) ta dùng công thức sau: (tức là: (số số hạng) = [(số cuối) – (số đầu)/[khoảng cách giữa 2 số liên tiếp]).
– Để tính tổng các số hạng cách đều nhau d đơn vị ta dùng công thức sau:
Tổng = [(số đầu số cuối)* (số số hạng)]/2
* Bài tập vận dụng
♦ Bài toán 1 : Cho tập hợp K = {12 ; 15 ; 18; 21; …; 111; 114 ; 117}
a) Tính số phần tử của tập hợp K
b) Tính tổng M = 12 +15 +18 +21 … +114 +117
♦ Bài toán 2 : Cho tập hợp A = {3; 5; 7; 9}. Điền các kí hiệu ∈, ∉, ⊂ thích hợp vào []
a) 5 [] A; b) 6 [] A; c) {3; 7} [] A; c) {3; 7 ; 9} [] A
♦ Bài toán 3 : Tính số phần tử của tập hợp sau
a) A = { x ∈ N / 8 < x < 27 }
b) B = { x ∈ N / 2018 0.x = 2018 }
♦ Bài toán 4 : Cho tập hợp M = { 8; 9; 10; …; 57}
a) Tìm số phần tử của tập hợp M ?
b) Viết tập hợp M bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp ?
c) Cho N = { 13 ; 15 ; 17 ; … ; 59}. Hỏi N có phải là tập con của M không ?
♦ Bài toán 5 : Tính tổng sau.
a) S = 1 +3 +5+ … +2015 +2017
b) S = 7 +11 +15 +19+ … +51 +55
c) S = 2 +4 6 +… +2016 +2018
III. Hướng dẫn giải các bài toán về tập hợp
° Dạng 1: Tìm số phần tử của 1 tập hợp
◊ Đáp án bài toán 1:
Liệt kê: A = {0;1;2;3;4} Chỉ ra tính chất đặc trưng: A = {x ∈ N | 0 ≤ x ≤ 4}
◊ Đáp án bài toán 2: Liệt kê: A = {6;7;8} Chỉ ra tính chất đặc trưng: A = {x ∈ N | 5 < x < 9}
◊ Đáp án bài toán 3: A = {0;1;2;3;4;5;6;7}; B = {0;1;2;3;4;5;6}; C = Ø
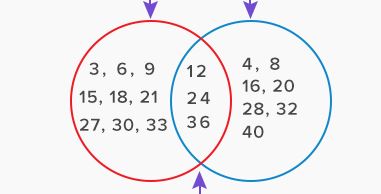
◊ Đáp án bài toán 4: a) A = {10; 12; 14; 16; 18; 20; 22; 24; 26}; B = {10; 15; 20; 25}
◊ Đáp án bài toán 5: A = {21; 24; 27; 30; 33; 36; 39} B = {25; 30; 35}
° Dạng 2: Tìm số phần tử của một tập hợp
◊ Đáp án bài toán 1:
a) Số phần tử của tập K (để ý các phần tử cách nhau 3 đơn vị) là: [(117-12)/3] 1 = 35 +1 = 36 (phần tử)
b) M = 12 +15 +18 +21 … +114 +117 = [(12 +117).36]/2 = 2322
◊ Đáp án bài toán 2: a) 5 ∈ A; b) 6 ∉ A; c) {3; 7} ⊂ A; c) {3; 7; 9} ⊂ A
◊ Đáp án bài toán 3: a) A = { x ∈ N / 8 < x < 27 } ={9; 10; 11; …; 26} ⇒ Số phần tử của A là (26-9) 1 = 18. b) B = {x ∈ N / 2018 0.x = 2018 } = {x ∈ N / 0.x = 0} = {x|x ∈ N} hay B = N. vô số phần tử.
◊ Đáp án bài toán 4:
a) Số phần tử của M: (57 – 8) +1 = 50
b) M = {x ∈ N | 8 ≤ x ≤ 57}
c) N không là tập con của M vì 59 ∈ N nhưng 59 ∉ M.
◊ Đáp án bài toán 5:
a) S = 1 +3 +5 … +2015 +2017
– Ta có: số số hạng của S (các số cách nhau 2 đơn vị) là: [(2017 – 1)/2] +1 = 1009
– Tổng: S = [(2017 +1).1009]/2 = 1018081.
b) S = 7 +11 +15 +19 … +51 +55
– Ta có: Số số hạng của S (các số cách nhau 4 đơn vị) là: [(55 – 7)/4] 1 = 13
– Tổng: S = [(55 +7).13]/2 = 403 c) S = 2 +4 +6 … +2016 +2018
– Ta có: Số số hạng của S (các số cách nhau 2 đơn vị) là: [(2018 – 2)/2] +1 = 1009
– Tổng: S = [(2018 +2).1009]/2 = 1019090.
Bài học/ Tin tức liên quan của bài học/tin tức trong bộ sách Chương trình hiện hành

11 dạng toán về phân số
Trong bài viết này chúng ta cùng ôn lại các kiến thức về phân số, các dạng toán về phân số để các em hiểu rõ...

Các dạng toán Tính tổng dãy số lũy thừa có quy luật – Số học 6
Tính tổng dãy số lũy thừa là một dạng toán khó trong chương trình Số học 6, Toán lớp 6. Để giải được đòi hỏi phải có phương...
Cách tìm số ước của một số
Để tìm số ước của một số cho trước, ta chỉ việc phân tích ước của một số. Sau đó lấy số mũ của các thừa số nguyên tố đó cộng với 1 rồi nhân...

Bài tập ôn chương 1: Bội, bội chung nhỏ nhất
Bài tập ôn chương 1: Bội, bội chung nhỏ nhất – Số học 6
Bài học/ Tin tức liên quan qua các bộ sách khác
BÀI 1: TẬP HỢP. PHẦN TỬ CỦA TẬP HỢP
Học sinh được làm quen với khái niệm tập hợp bằng cách lấy các ví dụ về tập hợp, nhận biết được một số đối tượng cụ thể thuộc hay không thuộc một tập hợp...

BÀI 2: TẬP HỢP CÁC SỐ TỰ NHIÊN
HS biết được tập hợp các số tự nhiên, nắm được quy ước về thứ tự trong tập hợp số tự nhiên, biết biểu diễn một số tự nhiên trên trục số, điểm biểu diễn số nhỏ nằm...

BÀI 1. TẬP HỢP. PHẦN TỬ CỦA TẬP HỢP
Hãy làm quen với tập hợp và các kí hiệu ∈ , ∉

BÀI 1: TẬP HỢP
- Nhận biết: + Một tập hợp và các phần tử của nó. +...

BÀI 2: CÁCH GHI SỐ TỰ NHIÊN
- Nhận biết được mối quan hệ giữa các hàng và giá trị mỗi chữ số ( theo vị trí) trong một số tự nhiên đã cho viết trong hệ thập phân....

BÀI 3: THỨ TỰ TRONG TẬP HỢP CÁC SỐ TỰ NHIÊN
- Nhận biết được tia số. - Nhận biết được thứ tự các số tự nhiên và mối liên hệ với các điểm biểu diễn chúng trên tia số.

Bài tập ôn chương 1: Ước, ước chung lớn nhất
Bài tập ôn chương 1: Ước, ước chung lớn nhất – Số học 6


