Chuyên mục
Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Bộ sách Chương trình hiện hànhBài 9: Hai đường thẳng song song và dấu hiệu nhận biết
- CÁC GÓC TẠO BỞI MỘT ĐƯỜNG THẲNG CẮT HAI ĐƯỜNG THẲNG
a, Góc so le trong, góc đồng vị
Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại các điểm A và B tạo thành 4 góc đỉnh A, bốn góc đỉnh B được đánh số như hình 3.16. Ta sắp xếp các góc thành từng cặp. Mỗi cặp gồm 1 góc đỉnh A và 1 góc đỉnh B.
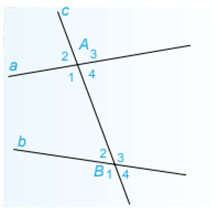
Hình 3.16
+ Các cặp góc A1 và B3 ; A4 và B2 được gọi là các cặp góc so le trong.
+ Các cặp góc A1 và B1 ; A2 và B2 ; A3 và B3 ; A4 và B4 được gọi là các cặp góc đồng vị.
* Mở rộng:
+ Các cặp góc A1 và B2 ; A4 và B3 được gọi là các cặp góc trong cùng phía
+ Các cặp góc A2 và B4 ; A3 và B1 được gọi là các cặp góc so le ngoài
? Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17).Em hãy kể tên:
a) Hai cặp góc so le trong
b) Bốn cặp góc đồng vị.
Hướng dẫn giải:
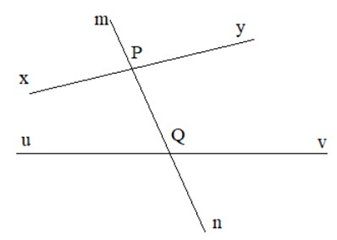
a) Hai cặp góc so le trong là: góc xPn và góc mQv; góc yPn và góc uQm
b) Bốn cặp góc đồng vị là: góc mPy và góc mQv; góc yPn và góc vQn; góc mPx và góc mQu; góc xPn và góc uQn.
HĐ 1
Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng 60o
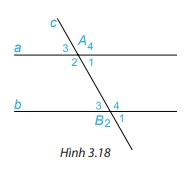
Hãy tính và so sánh hai góc so le trong còn lại A2 và B4.
Hướng dẫn giải:
+) Vì + =180o (2 góc kề bù)
⇒ 60o+ =180o
⇒ =180o − 60o = 120o
+) Vì + =180o (2 góc kề bù)
⇒ 60o + = 180o
⇒ = 180o − 60o = 120o
Vậy hai góc so le trong còn lại A2 và B4 bằng nhau và bằng 120o
HĐ 2
Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng 60o

Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.
Hướng dẫn giải:
Chọn cặp góc đồng vị: góc A1 và góc B4
Ta có: = 60O; =60O
= (2 góc đối đỉnh)
⇒ = 60O
b, Tính chất:
Nếu đường thẳng c cắt hai đường thẳng a,b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
* 2 góc so le trong còn lại bằng nhau
* 2 góc đồng vị bằng nhau
Luyện tập 1
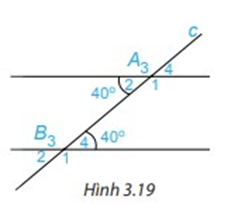
a) Cho hình 3.19, biết = 40O; = 40O. Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: + ; +
Hướng dẫn giải:
a) Vì + =180o (2 góc kề bù)
⇒ + 40o =180o
⇒ =180o – 40o = 140o
Ta có: = (2 góc đối đỉnh), mà = 140o
= (2 góc đối đỉnh), mà = 40o nên = 40o
Vì = = 40o, mà 2 góc này ở vị trí so le trong
⇒ 2 góc đồng vị bằng nhau nên
= =140o; = = 40o; = = 140o; = = 40o
b) Ta có:
+ = 140o + 40o = 180o, + = 40o + 140o = 180o
- DẤU HIỆU NHẬN BIẾT HAI ĐƯỜNG THẲNG SONG SONG
Để biết hai đường thẳng cắt nhau hay song song với nhau, ta cần biết chúng có điểm chung hay không. Việc kiểm tra trực tiếp, tức là xác định điểm chung của hai đường thẳng đã cho, trong nhiều trường hợp, là rất khó thực hiện. Chẳng hạn như trên hình 3.20a, không phải lúc nào ta cũng có thể kéo dài được hai đường thẳng c và d để tìm điểm chung của chúng. Vậy có cách nào thuận tiện hơn để nhận biết hai đường thẳng song song hay không?
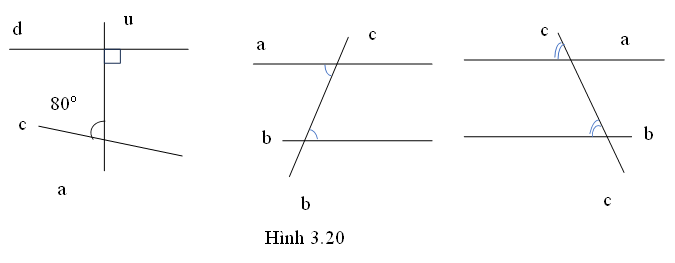
Định nghĩa: Nếu đường thẳng c cắt hai đường thẳng a,b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau (H3.20b,c).
Luyện tập 2
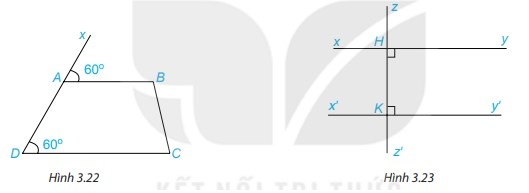
1. Quan sát Hình 3.22 và giải thích vì sao AB // CD.
2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song?
Hướng dẫn giải:
1. Vì = (60O) Mà 2 góc này ở vị trí đồng vị
⇒ AB//CD (Dấu hiệu nhận biết hai đường thẳng song song)
2. Ta có: + = 180o ( 2 góc kề bù)
⇒90o + = 180o ⇒ = 180o − 90o = 90o
Vì =
Mà 2 góc này ở vị trí đồng vị
⇒ xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song)
Nhận xét: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Thực hành 1
Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Để vẽ đường thẳng b đi qua A và song song với a, ta có thể sử dụng góc nhọn 60o của êke để vẽ như sau:
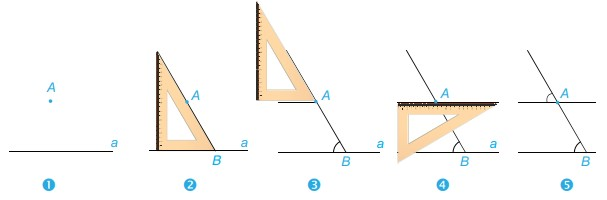
Tại sao khi vẽ như trên ta lại khẳng định được hai đường thẳng a và b song song với nhau.
Hướng dẫn giải:
Ta thấy, khi vẽ hình như trên, ta đã vẽ 2 góc A và B có số đo bằng nhau (đều bằng 60o)
Mà 2 góc này ở vị trí đồng vị
Vậy a//b (Dấu hiệu nhận biết 2 đường thẳng song song)
Thực hành 2
Dùng góc vuông hay góc 30o của êke (thay cho góc 60o) để vẽ đường thẳng đi qua và song song với đường thẳng a cho trước.
Hướng dẫn giải:
+ Dùng góc vuông:
Bước 1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a
Bước 2: Đặt ê ke sao cho 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, 1 cạnh góc vuông còn lại đi qua điểm A, ta kẻ đường thẳng b đi qua A, vuông góc với a.
Bước 3: Kẻ đường thẳng đi qua A, vuông góc với đường thẳng b.

Ta được đường thẳng b đi qua A và song song với a.
+ Dùng góc 30o của êke:
Bước 1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a
Bước 2: Đặt ê ke sao cho góc nhọn 30o và 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, cạnh đối diện với góc vuông đi qua điểm A, ta kẻ đường thẳng c đi qua cạnh đối diện với góc vuông của ê ke.
Bước 3: Dịch chuyển ê ke theo đường thẳng c cho đến khi điểm A trùng với đỉnh của góc nhọn 30o.
Bước 4: Kẻ đường thẳng b đi qua A và 1 cạnh của góc 30o

Ta được đường thẳng b đi qua A và song song với a.
BÀI TẬP
Bài 3.6:
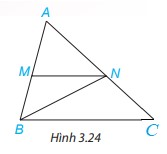
Quan sát hình 3.24:
a) Tìm một góc ở vị trí so le trong với góc MNB.
b) Tìm một góc ở vị trí đồng vị với góc ACB.
c) Kể tên một cặp góc trong cùng phía.
Hướng dẫn giải:
a) Góc MNB so le trong với góc NBC
b) Góc ACB đồng vị với góc ANM
c) Các cặp góc trong cùng phía là: góc MNC và góc NCB; góc NMB và góc MBC
Bài 3.7:
Quan sát Hình 3.25. Biết = 40o; =40O. Em hãy giải thích tại sao EF // NM.
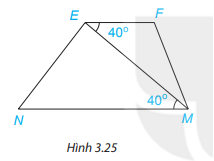
Hướng dẫn giải:
Vì = =40O
Mà 2 góc này ở vị trí so le trong
⇒ EF // NM ( Dấu hiệu nhận biết hai đường thẳng song song)
Bài 3.8:
Quan sát hình 3.26, giải thích vì sao AB // DC.
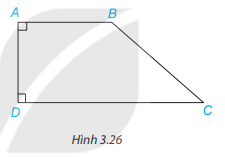
Hướng dẫn giải:
Vì AB và DC cùng vuông góc với đường thẳng AD nên AB // DC ( Theo nhận xét trang 48)
Bài 3.9:
Cho điểm A và đường thẳng d không đi qua A. Hãy vẽ đường thẳng d’ đi qua A và song song với d
Hướng dẫn giải:

+ Từ điểm A vẽ đường thẳng AB vuông góc với d
+ Tại điểm A vẽ đường thẳng Ad’ vuông góc với Ad. Ta được d//d’
Bài 3.10:
Cho hai điểm A và B. Hãy vẽ đường thẳng a đi qua A và đường thẳng b đi qua B sao cho a song song với b.
Vẽ đường thẳng b bất kì đi qua điểm B rồi vẽ đường thẳng a đi qua A và song song với b.
Hướng dẫn giải:
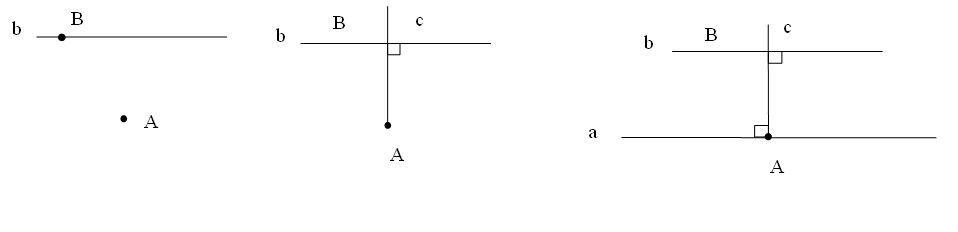
- Vẽ đường thẳng b bất kì đi qua điểm B
- Vẽ đường thẳng Ac đi qua A và vuông góc với b.
- Tại A vẽ đường thẳng a vuông góc với Ac. Ta được a//b (góc so le trong)
Bài 3.11
Hãy vẽ hai đoạn thẳng AB và MN sao cho AB // MN và AB = MN
Hướng dẫn giải:
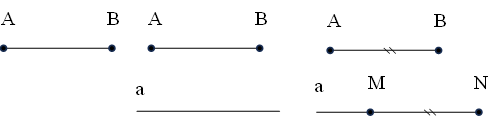
Bước 1: Vẽ đoạn thẳng AB
Bước 2: Vẽ đường thẳng a // AB
Bước 3: Trên a lấy điểm M và N sao cho MN = AB
Bài học/ Tin tức liên quan của bài học/tin tức trong bộ sách Chương trình hiện hành
BÀI 16: TAM GIÁC CÂN. ĐƯỜNG TRUNG TRỰC CỦA ĐOẠN THẲNG
* Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau. Trong hình 4.58, tam giác cân ABC (AB = AC) được gọi là...


